

Unfortunately, the reverence for ancient Greek philosophers meant their theories were widely applied without any testing to see if the theories applied to any given situation….as Gibson puts it in his notes, “had anyone bothered to build any of the instruments (except for the flute) in the ratios prescribed in the woodcut, they would have found that the intervals were all wrong.” The examples in the upper panels are even more complicated, but bells, water glasses, and anvils also would not produce the correct intervals. However, the panel on the lower left is problematic since the weights on the ends of the strings change their tension – as the frequency of the strings is not simply related to the tension, weighted strings will not sound in accordance with Pythagorean intervals. This works because, like a string, the frequency of an air column is simply related to its length. The lower right panel shows flutes whose lengths correspond to the Pythagorean ratios. This woodcut was made in the Middle Ages to explain illustrate Pythagorean ratios and how they applied to musical instruments:

Unfortunately, this is not true for the tension in a string, or for the length of vibrating bars such as those on a xylophone. So, all the conclusions he reached about ratios of lengths of strings for different intervals, also apply to the ratios of the frequencies in the intervals. Gibson of the University of Connecticut Pythagoras “got lucky”: he did not actually study the frequencies that made up pleasing intervals and the musical scale – he just made observations about the lengths of the strings that made intervals and scales, and by coincidence, the frequency of a string has a simple relationship to its length. Pythagoras was the first to identify that the pitch of a musical note is in inverse proportion to the length of the string that produces it.Īccording to Dr George N. This tuning approach suits other intervals better…while the Pythagorean approach works well tonally for fifths – a 3:2 ratio having a pleasing sound, other intervals such as thirds – 81:64 for major thirds and 32:27 for minor thirds sound much less pleasing, and as a result, Pythagorean tuning is rarely found after around 1510. “A above Middle C” is the benchmark note for which there is a definition in terms of physics, with a sound frequency now set at exactly 440 Hz. “Middle C” is the reference point for all the keys on a piano, and for the musical scale in general. This “equal semitones” approach was developed simultaneously in Europe and China in the 16 th century. This is close to, but not the same as 3:2 (1.5). Payne translation, Dover Publications, 1966, p.266īy considering a scale to consist of 12 equal intervals, a solution to stacking of the fifths can be found from the 12 th root…if the seventh octave is 128:1 or 2 7, then the fifth is 2 7/12 or 1.4983:1. – The World as Will and Representation, Volume I, §52, E.F.J. The numbers themselves, by which the tones can be expressed, have insoluable irrationalities,” “…thus, a perfectly pure harmonious system of tones is impossible not only physically, but even arithmetically. Although there is a suggestion that the Pythagoreans were unaware of this, the philosopher Arthur Schopenhauer, described the problem:
However, when extending this tuning however, a problem arises since no stack of 3:2 intervals (perfect fifths) will fit exactly into any stack of 2:1 intervals (octaves). These ratios harmonise musically as well as mathematically ie they are pleasing to the mind and the ear.
#MUSIC NOTE C IN HERTX HOW TO#
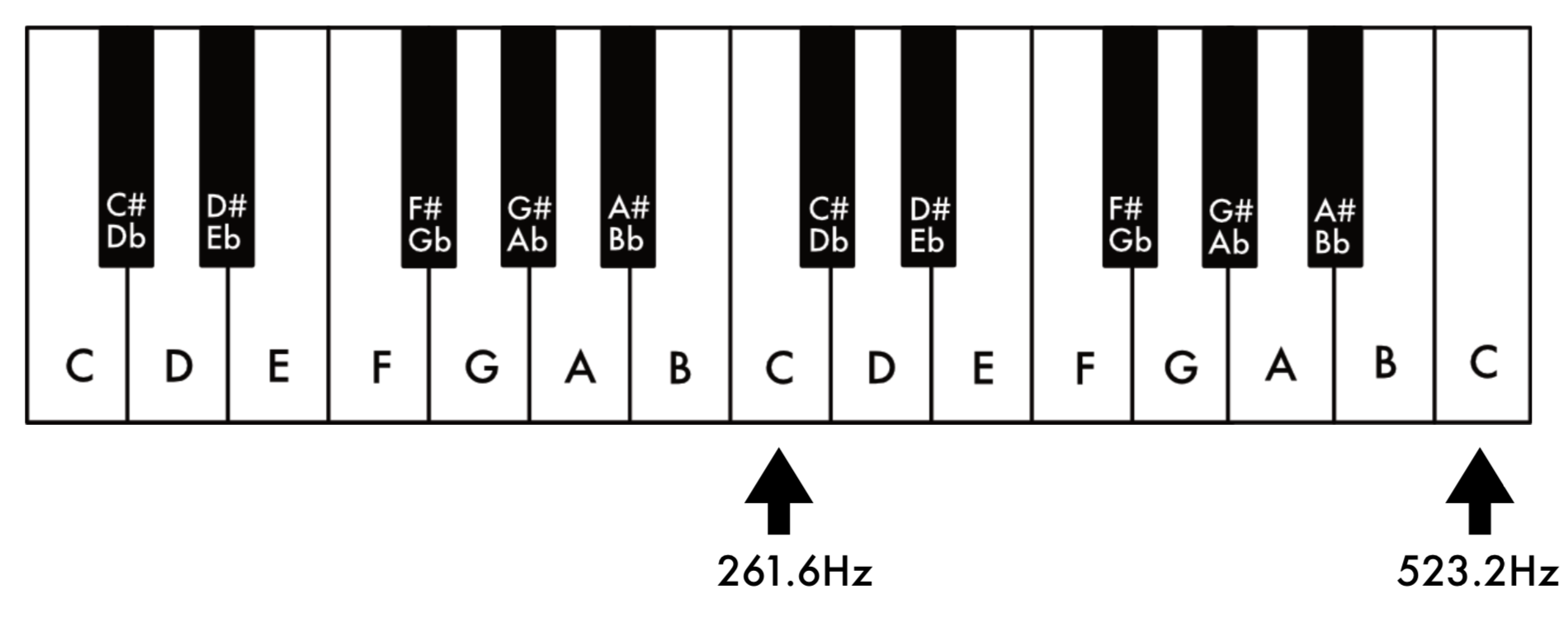
The ancient Greeks described music in terms of a seven-note scale, to which have been assigned the letters A through G, where the main intervals could be expressed as simple mathematical ratios between the first four integers, with: octave (eighth)=2:1, fifth=3:2, fourth=4:3 (the counting system was inclusive, of the original numbers, which is how to get eight notes in a seven-note system – the fourth and fifth reduce to three and four as numbers, which then do add up to seven).
#MUSIC NOTE C IN HERTX FULL#
This time of year is full of music, with carol singers out in force and the ubiquitous Christmas “hits” playing on loop in every store, but a recent discovery has brought music to mind in a different way… The music of the spheres – Pythagorean theory of the universe


 0 kommentar(er)
0 kommentar(er)
